独立な2群のt検定

平均値差の検定とは

これまでは，母集団$X$と標本$x$の関係に注目して検定を行いました． これからは，２つの標本（標本$x_1$，標本$x_2$）の関係に注目し， それぞれの平均値の有意な差があるかどうかを検定します． ２つの標本を検定する場合，下記の条件によって適用する手法が異なります．

• 独立な2群（対応のない2群）
• 対応のある2群

独立な2群（対応のない2群） とは，ある母集団から２つの標本を抽出したとき， それぞれの標本に含まれる対象が互いに無関係であることを意味しています． 例えば，下記のように，母集団$X$から8人の被験者を抽出して， これをランダムに4人の2群に分けた場合は，「独立な2群」です．

$x_1 = \{a,b,c,d\} \\ x_2 = \{e,f,g,h\}$

一方，対応のある2群 とは，2つの標本に含まれる対象に，何らかの対応関係があることを意味しています． 例えば，下記のように，同じ4人の被験者に対して，2種類の条件下で測定された2群のデータは，「対応のある2群」です．

$条件1: x_1 = \{a,b,c,d\} \\ 条件2: x_2 = \{a',b',c',d'\}$

今回は，前者の 独立な2群（対応のない2群） のt検定を解説します．

スクリプトの作成

コードを入力し保存するためのスクリプトを作成しましょう． [ファイル]-[新しいスクリプト]をクリックし，Rエディタを表示します． 次に，[ファイル]-[保存]をクリックして，スクリプトを保存します． このとき，ファイル名はchapter11としてください． また，ファイルの保存場所と作業ディレクトリをデスクトップに変更しておきます．

t検定の前提条件

独立な2群の平均値差の検定にもt検定を利用します． ただし，t検定を適用するには，下記の条件を満たす必要があります．

1. ランダムサンプリングにより標本が抽出されている
2. 母集団の分布が正規分布である
3. 母集団の分散が等質である

上記の条件1，2はこれまでの前提と同じですが，条件3が新しく追加されました． もし，条件3を満たさない場合は，t検定の代わりに，Welchの検定 を利用する必要があります． Welchの検定に関しては割愛します． ここでは，上記の全ての条件を満たしていると仮定して話を進めます．

独立な2群のt検定

それでは，下記の問題について考えていきましょう．

ここでは，2つの標本の平均値の差が問題となるため，

この$\mu_1 - \mu_2$は下記の正規分布に従います．

$\mu_1 - \mu_2 \sim N( \hat{\mu_1} - \hat{\mu_2}, \hat{\sigma}^2( \frac{1}{n_1} + \frac{1}{n_2}) )$

• 母集団の平均$\hat{\mu_1}，\hat{\mu_2}$
• 母集団の標準偏差$\hat{\sigma}$
• 標本のサンプル数$n_1=5，n_2=5$

ここで，母集団の平均$\hat{\mu_1}，\hat{\mu_2}$と 母集団の標準偏差$\hat{\sigma}$が出現します． 先に述べたように「母集団の分散が等質である」ことを前提としているため， 母集団の標準偏差は同じ値を用いることに注意してください．また，一般に母集団の分散は未知であることから， 標本の標準偏差$\sigma_1，\sigma_2$を含む下記の式を用いて推定します． この分散の推定値をプールした分散と呼びます．

$\hat{\sigma}^2 = \frac{(n_1 - 1) \sigma_1^2 + (n_2 - 1) \sigma_2^2}{n_1 + n_2 - 2}$

上記の分布を標準化すると，検定統計量であるtスコアは下記の式で表されます．

$t = \frac{(\mu_1 - \mu_2) - (\hat{\mu_1} - \hat{\mu_2})}{\sqrt{\hat{\sigma} ^2 (\frac{1}{n_1} + \frac{1}{n_2})}}$

一般に，帰無仮説は$\hat{\mu_1}=\hat{\mu_2}$であることから，

$t = \frac{\mu_1 - \mu_2}{\sqrt{\hat{\sigma} ^2 (\frac{1}{n_1} + \frac{1}{n_2})}}$

この平均値の差は，自由度が$n_1+n_2-2$の自由度のt分布に従います．

それでは，検定の手順に従って，上記の問題を解いていきましょう． まずは，帰無仮説 と 対立仮説 を立てます．

• 帰無仮説：2つの標本の母平均は等しい $\hat{\mu_1} = \hat{\mu_2}$
• 対立仮説：2つの標本の母平均は等しくない $\hat{\mu_1} \neq \hat{\mu_2}$

次に，検定統計量 と，信頼区間(棄却域) を定めます． 今回は，検定統計量は上記のtスコアとし，信頼度には「95%信頼度（5%棄却域）」を用いることにしましょう．

それでは，検定統計量であるtスコアを計算してみましょう． まずは，標本の平均$\mu_1，\mu_2$と 標準偏差$\sigma_1，\sigma_2$を求めます．

x1 <- c(63,75,72,67,71)
x2 <- c(70,56,64,56,64)
mu1 <- mean(x1)
mu2 <- mean(x2)
sigma1 <- sd(x1)
sigma2 <- sd(x2)
    
> mu1
[1] 69.6
> mu2
[1] 62
> sigma1
[1] 4.669047
> sigma2
[1] 6

次に，母集団の分散の推定値（プールした分散）を求めましょう． ここで求めた値は 標準偏差$\hat{\sigma}$ではなく， 分散$\hat{\sigma}^2$であることに注意してください．

n1 <- length(x1)
n2 <- length(x2)
pvar <- ((n1-1)*sigma1^2 + (n2-1)*sigma2^2) / (n1 + n2 - 2) 
    
> n1
[1] 5
> n2
[1] 5
> pvar
[1] 28.9

上記の計算結果を基ににtスコアを求めます．

t <- (mu1 - mu2) / sqrt(pvar * (1/n1 + 1/n2))
> t
[1] 2.235294

最後に，自由度$n1+n2-2=8$のt分布を利用して，帰無仮説が採択か棄却かを調べましょう． qt関数を用いると，95%信頼度のとき，t<-2.3，また，t>2.3 が棄却域となることが分かります．

> qt(0.025,8)
[1] -2.306004
> qt(0.975,8)
[1] 2.306004

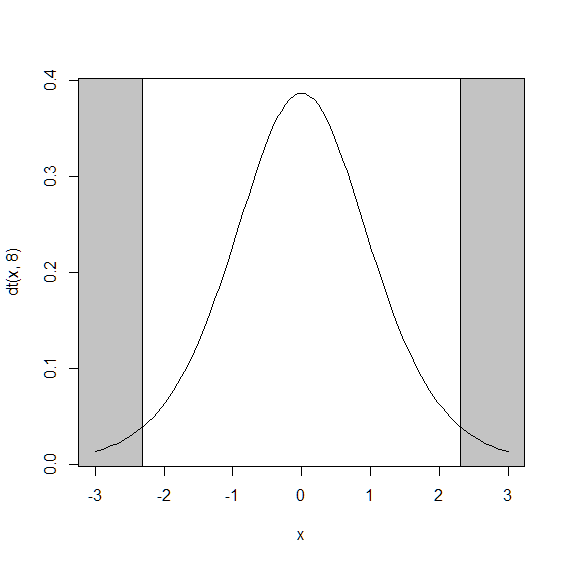
合わせてt分布をグラフにして確認してみましょう．

> curve(dt(x,8),-3,3)
> abline(v=qt(0.025,8))
> abline(v=qt(0.975,8))

上記の結果から，tスコアの2.24は棄却域に含まれないので， 帰無仮説「2つの標本の母平均は等しい」が採択されます． これは，向研究室の学生と見田研究室の学生の間には有意な差がないということを意味しています． これぐらいの差は偶然に起こり得るというわけです．

関数を利用したt検定

上記の検定はt.test関数でも可能です． 2つの標本の平均値差を検定するには，比較したい2つの標本を引数として与えるだけです． このとき，母分散が等質であることを表すvar.equal=TRUEというオプションも同時に指定します．

> t.test(x1,x2,var.equal=TRUE)

Two Sample t-test

data:  x1 and x2
t = 2.2353, df = 8, p-value = 0.05583
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.2404141 15.4404141
sample estimates:
mean of x mean of y 
    69.6      62.0 

tスコアが求めた2.24に一致していることが分かります． p値が0.05（5%）であることから，ぎりぎり95%信頼度に含まれたことが分かります． また，母集団の平均値差の信頼区間は -0.24 から 15.44 となっており， 帰無仮説である$\hat{\mu_1} - \hat{\mu_2}=0$が含まれていることが分かります．

課題

見田研究室の学生の得点が{65,55,52,45,51}だったときのtスコアを求めなさい． また，t検定を用いて，「95%信頼度（5%棄却域）」のときに， 「帰無仮説：2つの標本の母平均は等しい $\hat{\mu_1} = \hat{\mu_2}$」は棄却されるか調べ， そのときの母集団の平均値差の信頼区間も求めなさい． ソースはchapter11.Rに記述して提出すること．