畳み込みニューラルネットワーク
畳み込みニューラルネットワーク
畳み込みニューラルネットワーク(Convolutional Neural Network: CNN) は, 画像や動画の分類に用いられる特殊なニューラルネットワークです. CNNは, 畳み込み層(Convolutional Layer) , プーリング層(Pooling Layer) , 全結合層(Full Connected Layer) の3種類で構成されます.
入力画像は,畳み込み層に入力され,プーリング層を経て, 全結合層で集約され,最終的に画像の分類を出力します. この畳み込み層とプーリング層の処理は,複数回繰り返されることがあります. 畳み込み層では複数のフィルタを用いて画像の特徴量を抽出します. プーリング層では特徴を失わないように画像サイズを縮小します(ダウンサンプリング). 全結合層は多層パーセプトロンで用いられる一般的な層と同じです.
畳み込み層
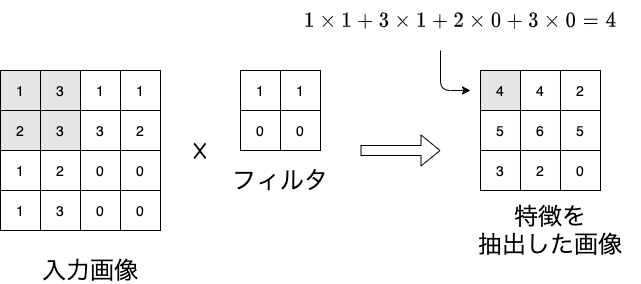
畳み込み層の仕組みを確認しましょう. 畳み込み層の目的は入力された複数の画像の特徴量をフィルタを利用して抽出することです. 下図は$4 \times 4$の入力画像に,$2 \times 2$のフィルタを適用した様子です. 入力画像からフィルタと同じ$2 \times 2$の画素を取り出し,フィルタの値と掛け合わせることで特徴量となります. この操作を1ピクセルだけずらしながら画像全体に適用すると$3 \times 3$の画像に変換されます. フィルタの値を変えることで,垂直方向の輪郭線や,水平方向の輪郭線を強調することが出来ます.
それでは,この畳み込み層の振る舞いを再現してみましょう.
ノートブックを作成し,ノートブックのタイトルをchapter6 に設定します. まずは,ライブラリのインストールとインポートを行います. ここでは,画像処理ライブラリのPillowと 数値計算ライブラリのScipyも追加します.
!pip install torch
!pip install torchvision
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from PIL import Image
前回と同じCIFAR-10データセットを利用します. また,簡単化のためRGB画像をグレースケール画像に変換します.
dataset = torchvision.datasets.CIFAR10(root="./data", download=True)
image, label = dataset[0]
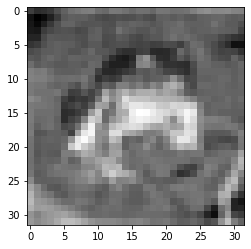
gray_image = image.convert('L') #グレースケールに変換
plt.imshow(gray_image, cmap="gray") #グレースケールとして表示
PIL.Image.Image を Numpy に変換します. $32 \times 32 $の行列でグレースケールの画素値が保持されています.
gray_image = np.asarray(gray_image)
print(gray_image.shape)
print(gray_image[0][0])
#出力
(32, 32)
61
水平方向の輪郭線を強調するための$3 \times 3$のフィルタを作成します.
$$
\left(
\begin{array}{ccc}
-1 & -1 & -1 \\\
2 & 2 & 2 \\\
-1 & -1 & -1
\end{array}
\right)\
$$
filter = np.array([[-1.0, -1.0, -1.0],[2.0, 2.0, 2.0],[-1.0, -1.0, -1.0]])
print(filter.shape)
print(filter)
#出力
(3, 3)
[[-1. -1. -1.]
[ 2. 2. 2.]
[-1. -1. -1.]]
signal.convolve2d()で2次元の畳み込みを行います.
出力画像は$30 \times 30$に縮小されることに注意してください.
converted_image = signal.convolve2d(gray_image, filter, mode="valid")
print(converted_image.shape)
#出力
(30, 30)
画像を Numpy から, PIL.Imgage.Image に戻して表示してみます. 水平方向の輪郭線に強く反応した画像が生成されていることが分かります.
converted_image = Image.fromarray(converted_image)
plt.imshow(converted_image, cmap="gray")
同様の操作で垂直の輪郭線を強調するフィルタを適用すると下記の画像となります.
$$
\left(
\begin{array}{ccc}
-1 & 2 & -1 \\\
-1 & 2 & -1 \\\
-1 & 2 & -1
\end{array}
\right)\
$$
このようにフィルタを複数用意することで,画像の異なる特徴を抽出することが可能です. 上記はグレースケール画像でしたが,RGB画像の場合は,3色(3チャネル)それぞれにフィルタが用意されます. また,抽出された特徴量は,多層パーセプトロンと同様に,バイアスを加えた後,活性化関数を適用して, 次のプーリング層に伝達されます.
プーリング層
プーリング層の仕組みを確認しましょう. プーリング層の目的は,画像サイズを縮小することで計算量を減らすことに加え, 画像中の認識対象の位置変化に対する柔軟性を向上させます(位置が違っても同じように認識できる).
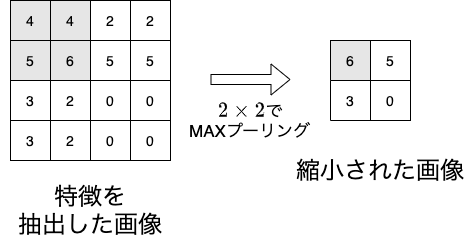
下図は$4 \times 4$の特徴量に,$2 \times 2$のMAXプーリングを適用した様子です. MAXプーリングは対象領域の最大値を代表値とする方法です. この値が全結合層に伝達され,全結合層で分類結果を出力します. プーリング層では重みやバイアスの学習は行われません.
ここでは,元の$32 \times 32$の画像にMAXプーリングを適用してみます(本来は畳み込み層の出力画像に適用する).
最初にプーリング後の値を記録する配列pooled_imageを用意します.
$2 \times 2$のMAXプーリングの適用後に画像サイズは$16 \times 16$になることに注意してください.
pooling_size = (2, 2)
image_size = gray_image.shape
pooled_image = np.zeros(((int)(image_size[1]/pooling_size[1]), (int)(image_size[0]/pooling_size[0]))) # 16x16の配列
$2 \times 2$の領域から,np.max()で最大値を選択し,pooled_imageに記録します.
平均プーリングの場合は,np.mean()を利用すればOKです.
# MAXプーリング
for y in range(pooled_image.shape[1]):
for x in range(pooled_image.shape[0]):
head_x = x * pooling_size[0]
head_y = y * pooling_size[1]
values = gray_image[head_y:head_y+pooling_size[1], head_x:head_x+pooling_size[0]]
pooled_image[y][x] = np.max(values) #最大値を選択
MAXプーリング後の画像とサイズを表示します. 元の画像の特徴が圧縮されていることがわかります.
converted_image = Image.fromarray(pooled_image)
print(converted_image.size)
plt.imshow(converted_image, cmap="gray")
#出力
(16, 16)
ネットワークの学習
それでは,畳込みニューラルネットワークを利用して,CIFAR-10の分類に挑戦しましょう.
transform=Transforms.ToTensor()オプションを設定して,
PyTorchで処理可能な形式でデータセットを読み込みます.
dataset = torchvision.datasets.CIFAR10(root="./data", transform=transforms.ToTensor())
今回も分類問題の難易度を下げるため, ラベルが0(airplane),1(automobile),2(bird)のみを対象とします.
my_dataset = []
for image, label in dataset:
if label == 0 or label == 1 or label == 2:
my_dataset.append((image, label))
これをバッチサイズ$n=64$のミニバッチ用のデータセットとします.
loader = torch.utils.data.DataLoader(dataset=my_dataset, batch_size=64)
4層で構成される畳み込みニューラルネットワークを定義します.
これまでの方法とは異なりnn.Moduleを継承した新しいクラスとして定義します.
コンストラクタである__init__で,畳み込み層1(conv1),畳み込み層2(conv2),
結合層1(fc1),結合層2(fc2)の順でネットワークの層を定義しています.
また,forward()でネットワークの順伝播の方法を定義しています.
畳み込み層はconv2d()で定義します.
畳み込み層1は,入力チャネル(RGBの3色)が$3$,出力チャネル(フィルタ数)が$6$,フィルタサイズが$5 \times 5$です.
畳み込み層2は,入力チャネル(フィルタ数)が$6$,出力チャネル(フィルタ数)が$16$,フィルタサイズが$5 \times 5$です.
また,MAXプーリングはF.max_pool2d()で定義します.
プーリングのサイズは$2 \times 2$に設定しています.
下図は畳み込み層1の処理を示しています.
フィルタごとに畳み込みが行われ,活性化関数ReLUを経て,6つの出力を生成します.
その後で,プーリング層でダウンサンプリングされ,畳み込み層2の入力として与えられます.
ここで,畳み込み層が出力する画像のサイズを考えます. 元の画像は$32 \times 32$ですが,畳み込み層1で$5 \times 5$のフィルタを適用することで, 画像の大きさは$28 \times 28$に縮小します. これを$2 \times 2$でプーリングすると,画像は$1/2$のサイズの$14 \times 14$に縮小します. さらに,畳み込み層2で$5 \times $5のフィルタを適用すると,画像の大きさは$10 \times 10$に縮小し, $2 \times 2$でプーリングすると$1/2$のサイズの$5 \times 5$に縮小します. この畳み込み層2の出力が,結合層1の入力となります.
結果的に,$16(フィルタ数) \times 5 \times 5 = 400$が結合層1の入力数になります(view()で1次元に変換してから入力).
これをもう一度,結合層2に伝搬・集約し,最終的にソフトマックスで各ラベルの確率を出力します.
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(3, 6, (5, 5)) #入力チャネル,出力チャネル,フィルタサイズ
self.conv2 = nn.Conv2d(6, 16, (5, 5)) #入力チャネル,出力チャネル,フィルタサイズ
self.fc1 = nn.Linear(16 * 5 * 5, 64) #入力数,出力数
self.fc2 = nn.Linear(64, 3) #入力数,出力数
def forward(self, x):
x = F.max_pool2d(F.relu(self.conv1(x)), 2) #2x2でMAXプーリング
x = F.max_pool2d(F.relu(self.conv2(x)), 2) #2x2でMAXプーリング
x = x.view(-1, 16 * 5 * 5) #1次元に整形
x = F.relu(self.fc1(x))
x = F.softmax(self.fc2(x), dim=1)
return x
network = Net()
print(network)
#出力
Net(
(conv1): Conv2d(3, 6, kernel_size=(5, 5), stride=(1, 1))
(conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(fc1): Linear(in_features=400, out_features=64, bias=True)
(fc2): Linear(in_features=64, out_features=3, bias=True)
)
ここで,学習データに対する正解率を確認してみます.
畳み込みニューラルネットワークの入力の形状は [バッチサイズ][チャネル数][縦][横] というテンソルになっている必要があるため,
torch.unsqueezeで次元を拡張し,バッチサイズ$n=1$のデータセットとして,入力していることに注意してください.
学習前であるため,$0.33$という低い正解率でした.
counter = 0
for image, label in my_dataset:
image = torch.unsqueeze(image, 0) #次元を増やす
z = network(image)
t = torch.argmax(z)
counter = counter+1 if (t == label) else counter
acc = counter / len(my_dataset)
print(acc)
#出力
0.3333333333333333
損失関数と最適化関数を定義します. 損失関数は ソフトマックス交差エントロピー , 最適化関数は Adam を採用しました.
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(network.parameters())
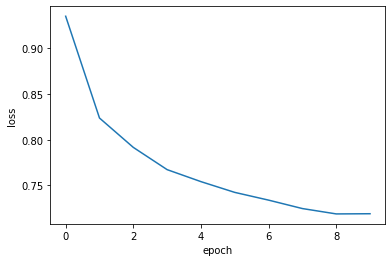
ミニバッチ学習を10エポック繰り返します. 損失の推移を可視化すると,エポックごとに損失が減少していることが確認できます.
loss_history = []
for epoch in range(10):
loss_epoch = 0
for i, (images, labels) in enumerate(loader):
optimizer.zero_grad()
z = network(images)
loss = criterion(z, labels)
loss.backward()
loss_epoch += loss.item()
optimizer.step()
print(f"{epoch} {loss_epoch / i}")
loss_history.append(loss_epoch / i)
#出力
0 0.9353420349777254
1 0.8237722921065795
2 0.7915834282707964
3 0.7671963142024146
4 0.7540506386858785
5 0.7422569465433431
6 0.7337749562202356
7 0.7245291201477377
8 0.7186577434723194
9 0.7188627052510905
plt.plot(loss_history)
plt.xlabel("epoch")
plt.ylabel("loss")
最後に正解率を再度計算してみましょう. あくまで学習データに対する正解率であり,評価用のデータではないことに注意). 正解率は0.846となり,前回の多層パーセプトロンよりも,高い正解率を実現できました.
counter = 0
for image, label in my_dataset:
image = torch.unsqueeze(image, 0) #次元を増やす
z = network(image)
t = torch.argmax(z)
counter = counter+1 if (t == label) else counter
acc = counter / len(my_dataset)
print(acc)
#出力
0.8462
課題
Google Colaboratoryで作成した chapter6.ipynb を保存し, 共有用のリンク と ノートブック(.ipynb) をダウンロードして提出してください. 提出の前に必ず下記の設定を行ってください.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定
- 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定