物体画像(CIFAR-10)の分類
物体画像(CIFAR-10)
CIFAR-10データセットを利用した物体画像の認識に挑戦しましょう. 60000枚のカラー画像(RGB)を含むデータセットであり, 各画像は$32 \times 32$ピクセルで構成されています. また,各画像は,airplane,automobile,birdなど10のカテゴリに分類されており, 前回学習した多層パーセプトロンを利用して分類を実現します.
ノートブックを作成し,ノートブックのタイトルをchapter5 に設定します. まずはPyTorch,Numpy,Matplotlibに加えて, データセットを提供するTorchvisionをインポートします. CIFAR-10も提供されるデータセットの一つです.
!pip install torch
!pip install torchvision
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import numpy as np
import matplotlib.pyplot as plt
それでは,CIFAR10のデータセットを読み込みます. 初回のみはローカルへのダウンロードが発生します. 今回は学習用に用いられる50000枚のデータを利用します.
dataset = torchvision.datasets.CIFAR10(root="./data", download=True)
print(dataset)
#出力
Extracting ./data/cifar-10-python.tar.gz to ./data
Dataset CIFAR10
Number of datapoints: 50000
Root location: ./data
Split: Train
データセットには,正解のラベルを表す番号が含まれていますが, ラベルの名前(例,airplane)などは含まれていません. そこで,ラベルの名前を含むリストを作成しておきます. リストの要素番号とラベルの番号が一致していることに注意してください.
label_names = np.array([
"airplane",
"automobile",
"bird",
"cat",
"deer",
"dog",
"frog",
"horse",
"ship",
"truck"])
データセットの最初のデータを取出します.
各データは画像(image)とラベル(label)のタプルで構成されています.
画像をplt.imshow()で表示してみましょう.
また,ラベルは6であり,対応するラベル名前はflogであることがわかります.
image, label = dataset[0]
plt.imshow(image)
print(type(image))
print(label)
print(label_names[label])
#出力
<class 'PIL.Image.Image'>
6
frog
上述で読み込んだ画像は PIL.Image.Image であり,
そのままPyTorchでは用いることができません.
そこで,transform=transforms.ToTensor()オプションを設定して,
再度,データセットを読み込みます.
dataset = torchvision.datasets.CIFAR10(root="./data", transform=transforms.ToTensor())
print(dataset)
#出力
Files already downloaded and verified
Dataset CIFAR10
Number of datapoints: 50000
Root location: ./data
Split: Train
StandardTransform
Transform: ToTensor()
データセットの最初のデータを取出します.
画像は torch.Tensor であり,PyTorchで処理できることが分かります.
また,$3 \times 32 \times 32$のテンソルで構成されており,
それぞれ,RGBの画素値,$X$座標,$Y$座標を表しています.
例えば,$X=10$,$Y=10$の赤色の画素値は0.3137であることが分かります.
image, label = dataset[0]
print(type(image))
print(image.size())
print(image[0][10][10])
print(label)
print(label_names[label])
#出力
<class 'torch.Tensor'>
torch.Size([3, 32, 32])
tensor(0.3137)
6
frog
ミニバッチ学習
これまでは,学習データの全てを用いて損失(誤差)を計算した後で, 重みやバイアスを1回更新するという方法を採用していました. この方法は バッチ学習 と呼ばれています. バッチ学習は,学習結果が安定しやすいという特徴がありますが, 一方で,局所解に陥りやすいという欠点があります. そこで,用いられるのが ミニバッチ学習 と呼ばれる方法です. $N$個の学習データから,ランダムに$n (\leq N)$個のデータを取り出し, これを用いて誤差を計算し,重みやバイアスの更新を複数回繰り返すという方法です. ランダムにデータを選んで学習を進めるため,局所解に陥りにくく, より良い解を発見できる可能性が向上します. 上記の$n$はバッチサイズと呼ばれます.
それでは,ミニバッチ学習用のデータセットを作成します. まずは,分類問題の難易度を下げるため, ラベルが0(airplane),1(automobile),2(bird)の3種類のみを抽出します. これにより,学習データの全データ数は$N=15000$となりました.
my_dataset = []
for image, label in dataset:
if label == 0 or label == 1 or label == 2:
my_dataset.append((image, label))
print(len(my_dataset))
#出力
15000
この$N=15000$からミニバッチ用の小さなデータセットを
torch.utils.data.DataLoader()を利用して作成します.
ここでは,バッチサイズ$n=64$としました.
loader = torch.utils.data.DataLoader(dataset=my_dataset, batch_size=64)
ネットワークの学習
4層で構成される多層パーセプトロンを定義します. ここでは,入力層は$3072=32 \times 32 \times 3$,中間層(2層目)は$600$, 中間層(3層目)は$600$,出力層は$3$のニューロンが配置されています. 出力層からは3つのラベル(airplane, automobile, bird)の確率が出力されます. また,活性化関数は,入力層と中間層は ReLU関数,出力層は Softmax関数 を利用しています. Softmax関数は下記の式で表され, 出力層が各ラベルの確率(割合)を出力するように調整する役割を担います.
$$ f(y_i) = \frac{\exp(y_i)}{\sum_i \exp(y_j)} $$
network = nn.Sequential(
nn.Linear(32 * 32 * 3, 600),
nn.ReLU(),
nn.Linear(600, 600),
nn.ReLU(),
nn.Linear(600, 3),
nn.Softmax(dim=1)
)
print(network)
#出力
Sequential(
(0): Linear(in_features=3072, out_features=600, bias=True)
(1): ReLU()
(2): Linear(in_features=600, out_features=600, bias=True)
(3): ReLU()
(4): Linear(in_features=600, out_features=3, bias=True)
(5): Softmax(dim=1)
)
ここで学習データに対する 正解率(Accuracy) を算出してみます. 当然,何も学習していないので,正解率は低く,0.321という結果でした.
counter = 0
for image, label in my_dataset:
image = image.view(-1, 32 * 32 * 3)
z = network(image)
t = torch.argmax(z)
counter = counter+1 if (t == label) else counter
acc = counter / len(my_dataset)
print(acc)
#出力
0.321
損失関数と最適化関数を定義します.
損失関数は ソフトマックス交差エントロピー,最適化関数は Adam を採用します.
ソフトマックス交差エントロピーは,多値分類問題で利用される損失関数であり,
nn.CrossEntropyLoss()で計算することができます.
この関数には出力結果$z$と,正解のラベル$\hat{z}$を引数として与えますが,
正解のラベルは One-Hot形式 (例. ${\bf \hat{z}}=(1,0,0)$ )ではなく,
ラベル形式 (例.$\hat{z}=0$)となることに注意してください.
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(network.parameters())
それでは,ミニバッチ学習を用いて重みとバイスを学習します.
バッチサイズは$n=64$としたため,1回のエポック(epoch)で
$15000 / 64 \simeq 234$回のミニバッチ学習が行わます.
これを10エポック繰り返します.
画像データ(image)をview()で1次元のテンソルに変換していることに注意してください.
loss_history = []
for epoch in range(10):
loss_epoch = 0
for i, (images, labels) in enumerate(loader):
images = images.view(-1, 32 * 32 * 3)
optimizer.zero_grad()
z = network(images)
loss = criterion(z, labels)
loss.backward()
loss_epoch += loss.item()
optimizer.step()
print(f"{epoch} {loss_epoch / i}")
loss_history.append(loss_epoch / i)
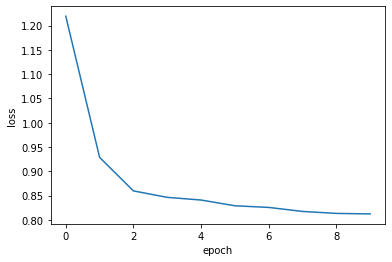
損失の推移を可視化します. エポックごとに損失が減少していることが確認できます.
#出力
0 1.2192253230983376
1 0.9285253609856988
2 0.8595439547147506
3 0.846264493261647
4 0.840729504568964
5 0.8289006696297572
6 0.8255122416039817
7 0.8172445302335625
8 0.8131960273807884
9 0.8121428805538732
plt.plot(loss_history)
plt.xlabel("epoch")
plt.ylabel("loss")
最後に正解率を再度計算してみましょう(あくまで学習用データに対する正解率であり,評価用のデータではないことに注意). 正解率は0.752となり,初期状態の0.321に比べ,かなり向上したことが確認できます.
counter = 0
for image, label in my_dataset:
image = image.view(-1, 32 * 32 * 3)
z = network(image)
t = torch.argmax(z)
counter = counter+1 if (t == label) else counter
acc = counter / len(my_dataset)
print(acc)
#出力
0.7523333333333333
課題
Google Colaboratoryで作成した chapter5.ipynb を保存し, 共有用のリンク と ノートブック(.ipynb) をダウンロードして提出してください. 提出の前に必ず下記の設定を行ってください.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定
- 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定