多層パーセプトロン

多層パーセプトロン

前回，単純パーセプトロンは分類問題に適用できることを確認しました． しかし，線形分離不可能問題（非線形な決定境界） を解くことが出来ないことが知られています． まずは，線形分離不可能問題（非線形な決定境界）について考えましょう．

ノートブックを作成し，ノートブックのタイトルをchapter4 に設定します． 前回と同様にPyTorchをインストールし，PyTorch，Numpy，Matplotlibをインポートします．

!pip install torch
!pip install torchvision

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
import itertools

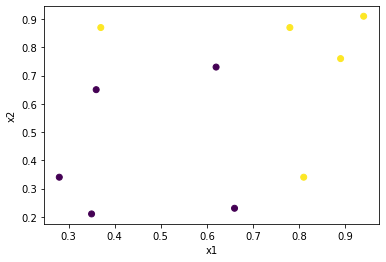
サンプル$x=(x_1, x_2)$を2つのカテゴリに分類します． 下記が今回の学習データであり， 決定境界を 直線 で引くことができないことが分かります． このような分類問題は単純パーセプトロンでは解くことが出来ません．

x1 = torch.tensor([0.28, 0.35, 0.36, 0.37, 0.62, 0.66, 0.78, 0.81, 0.89, 0.94], dtype=torch.float)
x2 = torch.tensor([0.34, 0.21, 0.65, 0.87, 0.73, 0.23, 0.87, 0.34, 0.76, 0.91], dtype=torch.float)
x = torch.stack([x1, x2], 1)
label = torch.tensor([0, 0, 0, 1, 0, 0, 1, 1, 1, 1], dtype=torch.float)
plt.scatter(x1, x2, c=label)
plt.xlabel("x1")
plt.ylabel("x2")

そこで，複数の層で構成した 多層パーセプトロン（ニューラルネットワーク） が考えられました． 多層パーセプトロンは少なくとも3つの層から構成され， それぞれ 入力層，中間層，出力層 と呼ばれます． また，各層には1つ以上のニューロンが配置されます． 異なる層のニューロン同士が結合され， あるニューロンの出力を，結合されたニューロンの入力として伝搬させるという特徴があります．

下図は2入力・1出力の多層パーセプトロンです． 入力層は$m=2$，中間層は$n=4$，出力層は$o=1$のニューロンが配置されています． 入力層から出力層に向けて情報を伝播することを 順伝播 ， 逆に，出力層から入力層に向けて情報が伝播することを 逆伝播 と呼びます．

ここで，入力層と中間層に注目します． 入力層と中間層のニューロンの全ての組み合わせに対して， 重み${\bf w}$が存在することになります（バイアスは考慮していないことに注意してください）． このため，重み${\bf w}$は $m \times n = 2 \times 4 = 8$ の要素で構成される 行列 として表現されます．

$$ {\bf w}= \left( \begin{array}{ccc} w_{11} & w_{12} & w_{13} & w_{14}\\\
w_{21} & w_{22} & w_{23} & w_{24} \end{array} \right) $$

また，入力${\bf x}=(x_1, x_2)$であるため，中間層の中間出力${\bf y}$は下記のようになります．

$$ {\bf y} = {\bf x} \cdot {\bf w} = (x_1, x_2) \cdot \left( \begin{array}{ccc} w_{11} & w_{12} & w_{13} & w_{14}\\\
w_{21} & w_{22} & w_{23} & w_{24} \end{array} \right) \\\
= (w_{11} x_1 + w_{21} x_2, w_{12} x_1 + w_{22} x_2, w_{13} x_1 + w_{23} x_2, w_{14} x_1 + w_{24} x_2) $$

この中間出力${\bf y}$に活性化関数$f$を適用し，中間層の最終的な出力とします (活性化関数には単純パーセプトロンと同様にシグモイド関数やReLU関数が用いられます)． 上記と同様の操作を出力層においても適用し，出力層の出力$z$を得ます．

多層パーセプトロンの学習

多層パーセプトロンの学習には，バックプロパゲーション（誤差逆伝播法） と呼ばれる方法を用います． この方法では，単純パーセプトロンの学習方法として紹介した 勾配降下法 をベースとした 最適化アルゴリズム を利用して， 誤差を出力から入力に向けて逆伝播させて，誤差を最小化するような重みやバイアスを導出します (誤差には単純パーセプトロンと同様に平均2乗誤差や交差エントロピーが用いられます)．

代表的な最適化アルゴリズムは下記です．

• 勾配降下法(Gradient Descent: GD)
• 確率的勾配降下法(Stochastic Gradient Descent: SGD)
• Momentum
• Adam

これら最適化アルゴリズムの詳細は割愛しますが， 近年はKingma氏らが2014年に提案したAdamが 高い性能を示すことで知られています． omiita氏の【2020決定版】スーパーわかりやすい最適化アルゴリズム の記事も参考にすると良いです．

パーセプトロンの定義

3層で構成される多層パーセプトロンを定義します． 入力層は$2$，中間層は$4$，出力層は$1$のニューロンが配置されています． また，中間層と出力層の活性化関数は シグモイド関数 を用いています．

# 多層パーセプトロン
network = nn.Sequential(
    nn.Linear(2, 4),
    nn.Sigmoid(),
    nn.Linear(4, 1),
    nn.Sigmoid()
)

print(network)

#出力
Sequential(
  (0): Linear(in_features=2, out_features=4, bias=True)
  (1): Sigmoid()
  (2): Linear(in_features=4, out_features=1, bias=True)
  (3): Sigmoid()
)

定義した多層パーセプトロンに学習データ${\bf x}$を入力として与えてみます． 重みやバイアスはランダムに初期化されており，学習前に正しく分類することは出来ません（当たり前ですが）．

z = network(x)
print(z)

#出力
tensor([[0.3961],
        [0.3961],
        [0.3973],
        [0.3978],
        [0.3988],
        [0.3980],
        [0.3996],
        [0.3990],
        [0.4000],
        [0.4003]], grad_fn=<SigmoidBackward>)

損失関数

前回説明したように損失関数には 平均2乗誤差 や 交差エントロピー が用いられます． 今回は2クラス分類に適しているとされる バイナリ交差エントロピー（Binary Cross Entoropy: BCE） を採用してみます． この損失関数はベルヌーイ分布を仮定したときの出力$z$の対数尤度を表し，下記の式で与えられます． ここで，$z$は出力，$\hat{z}$は正しい出力です．

$$ BCE = -\frac{1}{n} \sum_i ( \hat{z_i} \cdot \log(z_i) + (1-\hat{z_i}) \cdot log(1 - z_i)) $$

nn.BCELoss()でバイナリ交差エントロピーの計算グラフを作成します． 先程，得られた出力$z$と正しい出力$\hat{z}$（ここではlabel）を与えると， 損失は0.7121と計算されました．

# 損失関数
criterion = nn.BCELoss()
label = label.view(10, 1) # 10行1列に変換
loss = criterion(z, label)
print(loss)

#出力
tensor(0.7121, grad_fn=<BinaryCrossEntropyBackward>)

最適化関数

最適化関数として評価の高い Adam を採用します． optim.Adam()に定義した多層パーセプトロンのパラメータを引数に与えて初期化します．

# 最適化関数
optimizer = optim.Adam(network.parameters())
print(optimizer)

#出力
Adam (
Parameter Group 0
    amsgrad: False
    betas: (0.9, 0.999)
    eps: 1e-08
    lr: 0.001
    weight_decay: 0
)

多層パーセプトロンの学習

それではバックプロパゲーションで多層パーセプトロンを学習します． ここでは，20000回繰り返して重みとバイアスの更新を行います． optimizer.zero_grad()は計算済みの勾配をクリアするメソッドです． また，optimizer.step()はパラメータ（重みやバイアス）を更新するメソッドです．

loss_history = []

for i in range(0, 20000):

    optimizer.zero_grad()
    z = network(x)

    loss = criterion(z, label)
    loss.backward()

    loss_history.append(loss.data)

    optimizer.step()

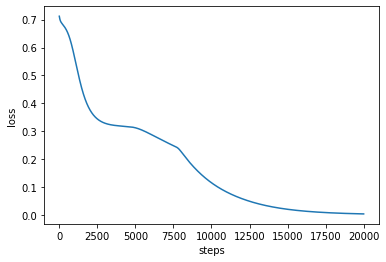
更新の過程における損失（バイナリ交差エントロピー）の推移を確認してみましょう． 20000ステップには$BCE \simeq 0$に収束していることが確認できます．

plt.plot(loss_history)
plt.xlabel("steps")
plt.ylabel("loss")

学習した多層パーセプトロンが正しく分類できているか確認しましょう． 学習データと同じ出力が得られていることが確認できます． 多層パーセプトロンが線形分離不可能問題に適用できることが分かりました．

z = network(x)
z = z.transpose(0,1)[0]
z = z.detach().numpy()
print(np.round(z))

#出力
[0. 0. 0. 1. 0. 0. 1. 1. 1. 1.]

最後に決定境界を確認します． $0<x1<1$，$0<x2<1$の範囲で多層パーセプトロンの出力を計算し， その値に応じてラベルを設定します． 下図のように非線形の決定境界が得られていることが確認できます．

import itertools

boundary = []

for x1_, x2_ in itertools.product(np.arange(0, 1, 0.01), np.arange(0, 1, 0.01)):
    x = torch.tensor([x1_, x2_], dtype=torch.float)
    z = network(x)
    t = 1 if z>= 0.5 else 0
    boundary.append([x1_, x2_, t])            

boundary = np.array(boundary).T

plt.scatter(boundary[0], boundary[1], c=boundary[2])

課題

Google Colaboratoryで作成した chapter4.ipynb を保存し， 共有用のリンク と ノートブック（.ipynb） をダウンロードして提出してください． 提出の前に必ず下記の設定を行ってください．

• ノートブックの設定で「セルの出力を除外する」のチェックを外す
• ノートブックの変更内容を保存して固定
• 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定