パーセプトロンの学習
自動微分
PyTorchでは 自動微分 という機能が実装されており, テンソルで作成した式( 計算グラフ と呼ぶ)の傾き(勾配)が保持されます. この自動微分はパーセプトロンの重みやバイアスの学習に欠かせない機能です.
ノートブックを作成し,ノートブックのタイトルをchapter3 に設定します. まずは,PyTorchをインストールし,PyTorch,Numpy,Matplotlibをインポートします.
!pip install torch
!pip install torchvision
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
テンソルxを2.0で初期化します.
このxを自動微分の対象とするためrequires_grad=Trueをオプションとして設定します.
x = torch.tensor([2.0], requires_grad=True) # x=2
print(x)
#出力
tensor([2.], requires_grad=True)
定義したxを用いて計算グラフyを定義します.
ここで,$x=2$であるため,$y=9$となります.
$$ y = x^2 + 2x + 1 $$
y = x * x + 2 * x + 1
print(y)
#出力
tensor([9.], grad_fn=<AddBackward0>)
yをxで微分します.
計算グラフが複数のテンソルで構成される場合は,
全てのテンソルに対する偏微分が計算されます.
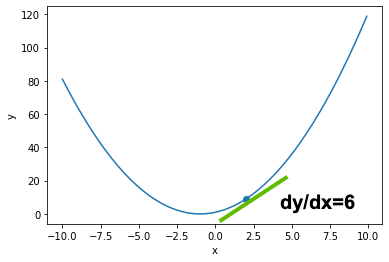
ここで,$x=2$であるため,$\frac{dy}{dx}=6$となります.
$$ \frac{dy}{dx} = 2x + 2 $$
y.backward() #微分
print(f"dy/dx = {x.grad}")
#出力
dy/dx = tensor([6.])
図で確認してみましょう. 微分は接線の傾きを求める操作です. $y = x^2 + 2x + 1$の$x=2$における接線の傾きが$6$となります.
パーセプトロンの学習
分類問題
パーセプトロンは 分類 や 回帰 と呼ばれる問題を解くことができます. ここでは,サンプル$x=(x_1, x_2)$を2つのカテゴリ(0または1)に分類することに挑戦します.
例えば,リストの最初にある$(0.28, 0.34)$はカテゴリ$0$に分類されます. 同様にリストの最後の$(0.94, 0.91)$はカテゴリ$1$に分類されます. このサンプルをパーセプトロンに学習させることで,任意のサンプルに対するカテゴリを推定します. このようなサンプルデータは 学習データ(教師データ,訓練データ) と呼ばれます.
x1 = torch.tensor([0.28, 0.35, 0.41, 0.78, 0.89, 0.94], dtype=torch.float)
x2 = torch.tensor([0.34, 0.21, 0.39, 0.87, 0.76, 0.91], dtype=torch.float)
x = torch.stack([x1, x2], 1) #入力
label = torch.tensor([0, 0, 0, 1, 1, 1], dtype=torch.float) #正解の出力
print(x)
print(label)
#出力
tensor([[0.2800, 0.3400],
[0.3500, 0.2100],
[0.4100, 0.3900],
[0.7800, 0.8700],
[0.8900, 0.7600],
[0.9400, 0.9100]])
tensor([0., 0., 0., 1., 1., 1.])
学習データを可視化してみます. 左下の3つのサンプルがカテゴリ$0$,右上の3つのサンプルがカテゴリ$1$です.
plt.scatter(x1, x2, c=label)
plt.xlabel("x1")
plt.ylabel("x2")
損失関数(誤差関数)
パーセプトロンに学習データを用いて 学習 させるには, パーセプトロンの出力$z$と正しい出力(ここでは$0$または$1$)との 誤差を測る必要があります.
この誤差を測るための関数は 損失関数(誤差関数) と呼ばれます. 損失関数には下記のような種類があります.
- 平均2乗誤差(Mean Square Error : MSE)
- 交差エントロピー(Cross Entropy : CE)
ここでは下記の式で表される平均2乗誤差を損失関数$L$として採用します. ここで,$z_i$は$i$番目のパーセプトロンの出力,$\hat{z_i}$は正しい出力です. また,$n$は学習データのサンプル数です.
$$ L = \frac{1}{n} \sum_i (z_i - \hat{z_i})^2 $$
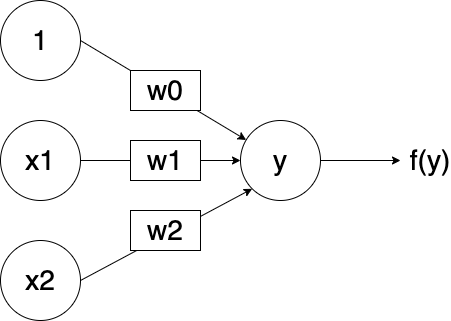
それでは,前回と同じ2入力・1出力の単純パーセプトロンを作成します. 活性化関数にはシグモイド関数を採用します.
# 単純パーセプトロン
network = nn.Sequential(
nn.Linear(2, 1),
nn.Sigmoid()
)
print(network)
#出力
Sequential(
(0): Linear(in_features=2, out_features=1, bias=True)
(1): Sigmoid()
)
学習データをパーセプトロンに入力し,出力を確認してみます. パーセプトロンの重みやバイアスはランダムな値で初期化されているため, 正解の出力とは大きく異ることが分かります. 例えば,$(0.28, 0.34)$を入力すると,$0.4417$が出力されています(正解の出力は$0$).
z = network(x)
z = z.transpose(0, 1)[0] # リストに変形
print(z)
#出力
tensor([0.4417, 0.4198, 0.4390, 0.4758, 0.4533, 0.4696],
grad_fn=<SelectBackward>)
平均2乗誤差の計算グラフをnn.MSELoss()で作成します.
この計算グラフにパーセプトロンの出力$z$と,正しい出力$\hat{z}$(ここではlabel)を与えると,
平均2乗誤差は$0.2365$と計算されました.
criterion = nn.MSELoss()
loss = criterion(z, label)
print(loss)
#出力
tensor(0.2365, grad_fn=<MseLossBackward>)
公式に従って計算し,上記の値が正しいか確認してみましょう. 平均2乗誤差は$0.2365$となり,一致していることが分かります.
print(torch.sum((z - label) ** 2) / 6)
#出力
tensor(0.2365, grad_fn=<DivBackward0>)
勾配降下法
平均2乗誤差で表された損失関数$L$を微分(偏微分)し, パーセプトロンの重み$(w_1, w_2)$やバイアス$(w_0)$に応じた 傾き(勾配) を求めます.
$$ \frac{dL}{dw_0}, \frac{dL}{dw_1}, \frac{dL}{dw_2} $$
正しい出力$\hat{z}$を得るために,導出した傾きに応じて重みやバイアスを微調整します. この方法は 勾配降下法 と呼ばれます.
平均2乗誤差の計算グラフをbackward()で微分します.
導出された傾きは下記のようになりました.
$$
\frac{dL}{dw_0} = -0.0264 \\
\frac{dL}{dw_1} = -0.0787 \\
\frac{dL}{dw_2} = -0.0788
$$
loss.backward()
print(network[0].weight) # 重みw1、w2
print(network[0].weight.grad) # 重みの偏微分 dL/dw1 dL/dw2
print(network[0].bias) # バイアス w0
print(network[0].bias.grad) # バイアスの偏微分 dL/dw0
#出力
Parameter containing:
tensor([[-0.2890, 0.5321]], requires_grad=True)
tensor([[-0.0787, -0.0788]])
Parameter containing:
tensor([-0.3343], requires_grad=True)
tensor([-0.0264])
導出した傾きに応じてパーセプトロンの重みやバイアスを下記の更新式に従って微調整します. ここで,$\alpha=0.1$は 学習率 と呼ばれるパラメータで,学習の収束をコントールする役割を担っています. この微調整により損失関数$L$を最小化することができます.
$$
w_0 = w_0 - \alpha \cdot \frac{dL}{dw_0} \\
w_1 = w_1 - \alpha \cdot \frac{dL}{dw_1} \\
w_2 = w_2 - \alpha \cdot \frac{dL}{dw_2}
$$
def update():
alpha = 0.1
weight = network[0].weight - alpha * network[0].weight.grad
bias = network[0].bias - alpha * network[0].bias.grad
network[0].weight.data[0] = weight
network[0].bias.data = bias
update()
print(network[0].weight)
print(network[0].bias)
#出力
Parameter containing:
tensor([[-0.2811, 0.5399]], requires_grad=True)
Parameter containing:
tensor([-0.3317], requires_grad=True)
それでは,1000回繰り返して重みとバイアスの更新を行います. この結果,重みとバイアスは下記の値に収束しました.
$$
w_0 = -130.2439 \\
w_1 = 117.0642 \\
w_2 = 122.1144
$$
loss_history = []
for i in range(0, 1000):
z = network(x)
z = z.transpose(0, 1)[0]
criterion = nn.MSELoss()
loss = criterion(z, label)
loss_history.append(loss.data)
loss.backward()
update()
print(network[0].weight)
print(network[0].bias)
#出力
Parameter containing:
tensor([[117.0642, 122.1144]], requires_grad=True)
Parameter containing:
tensor([-130.2439], requires_grad=True)
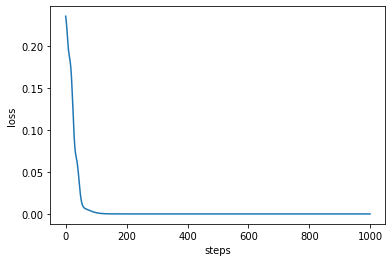
更新の過程における損失$L$(平均2乗誤差)の推移を可視化してみましょう. 100回程度の繰り返しで,$L \simeq 0$に収束していることが確認できます.
plt.plot(loss_history)
plt.xlabel("steps")
plt.ylabel("loss")
学習したパーセプトロンが正しく分類できているか確認しましょう. 前方の3つのサンプルの出力は$0$,後方の3つのサンプルの出力は$1$になっていることが確認できます.
z = network(x)
z = z.transpose(0, 1)[0]
print(z)
#出力
tensor([5.0410e-25, 2.3279e-28, 9.1925e-16, 1.0000e+00, 1.0000e+00, 1.0000e+00],
grad_fn=<SelectBackward>)
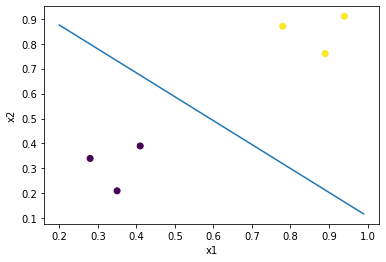
最後に決定境界を求めてみましょう. 途中出力$y$が$0$のときに決定境界となるため下記の式を解きます(シグモイド関数の出力が$0.5$のとき). 導出された式は2つのカテゴリを分ける直線となっていることが分かります.
$$
0 = w_1 \cdot x_1 + w_2 \cdot x_2 + w_0 \\
x_2 = -\frac{w_1}{w_2} x_1 - \frac{w_0}{w_2}
$$
x_ = np.arange(0.2, 1.0, 0.01)
y_ = []
w0 = network[0].bias.data[0]
w1 = network[0].weight.data[0][0]
w2 = network[0].weight.data[0][1]
for x in x_:
y_.append(-1 * (w1 / w2) * x -1 * (w0 / w2))
plt.plot(x_, y_)
plt.scatter(x1, x2, c=label)
plt.xlabel("x1")
plt.ylabel("x2")
課題
Google Colaboratoryで作成した chapter3.ipynb を保存し, 共有用のリンク と ノートブック(.ipynb) をダウンロードして提出してください. 提出の前に必ず下記の設定を行ってください.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定
- 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定