単純パーセプトロン
単純パーセプトロン
パーセプトロン とは,動物の神経細胞(ニューロン)の発火現象を数理的に表現したモデルのことです. ウォーレン・マカロック氏とウォルター・ピッツ氏が提案した 形式ニューロン を2層のネットワーク状に接続したものは 単純パーセプトロン と呼ばれます. 単純パーセプトロンの1層目のニューロンは,入力データを伝えるだけの役割であるため,実質的には1つの形式ニューロンと考えることができます.
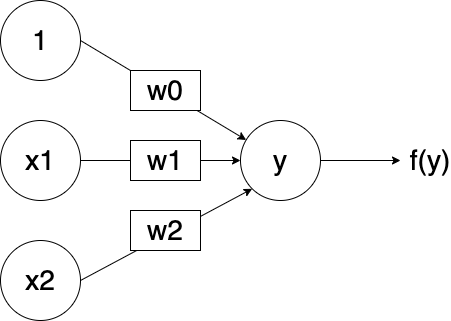
ここでは,2入力,1出力の単純パーセプトロンを考えます. 下記の式に従って,入力された$x_1$と$x_2$から,中間出力$y$を得ます. ここで,$w_1$と$w_2$は入力に対する 重み です. また,$w_0$は バイアス と呼ばれ,出力の閾値として用いられます.
$$ y = w_1 \times x_1 + w_2 \times x_2 + w_0 $$
この中間出力$y$に対して,活性化関数 $f$と呼ばれる特殊な関数を適用して, 得られた値を最終的なニューロンの出力$z$とします.
$$ z = f(y) $$
一般に$n$入力の単純パーセプトロンは,入力${\bf x}$と重み${\bf w}$は下記のようにベクトルで表現されます. ここで,$x_0=1$はバイアス$w_0$を導入するために用いられます. パーセプトロンが多層になると,ベクトル表現が必須となりますので,慣れておきましょう.
$$
{\bf x} = (1, x_1, \cdots, x_n) \\
{\bf w} = (w_0, w_1, \cdots, w_n) \\
y = {\bf x} \cdot {\bf w} \\
z = f(y)
$$
活性化関数$f$には下記のような種類があります.
- ステップ関数
- シグモイド関数
- ReLU(Rectified Linear Unit)関数
下図はステップ関数のグラフです. ステップ関数は入力$y$が0以上なら1,0未満であれば0を出力する関数です.
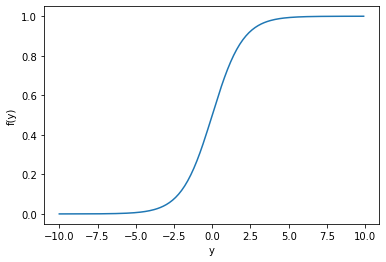
下図はシグモイド関数のグラフです. シグモイド関数は,ステップ関数とは異なり滑らかに変化する連続関数であり, 0から1の範囲を出力します.
$$ f(y) = \frac{1}{1 + e^{-y}} $$
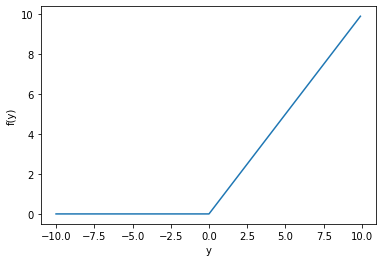
下図はReLU関数のグラフです. ReLU関数は入力$y$が0以上なら入力$y$をそのまま出力し, 0未満であれば0を出力する関数です.
単純パーセプトロンの実装
ノートブックを作成し,ノートブックのタイトルをchapter2 に設定します. それでは,単純パーセプトロンを PyTorch を利用して実装してみましょう. まずは,PyTorchをインストールし,PyTorchとNumpyをインポートします.
!pip install torch
!pip install torchvision
import torch
import torch.nn as nn
import numpy as np
単純パーセプトロンのネットワークを生成します.
nn.Sequentialは,パーセプトロンの層を追加した順番に並べます.
最初に2入力・1出力の層nn.Linear(2, 1)を作成します.
その出力をシグモイド関数nn.Sigmoid()に伝え,最終的な出力を得ています.
# 単純パーセプトロン
network = nn.Sequential(
nn.Linear(2, 1),
nn.Sigmoid()
)
print(network)
#出力
Sequential(
(0): Linear(in_features=2, out_features=1, bias=True)
(1): Sigmoid()
)
重みやバイアスなどのパラメータ$w$は,ランダムに初期化されています. ここでは,下記のようにパラメータを強制的に変更します.
$$ {\bf w} = (w_0, w_1, w_2) = (-0.5, 0, 1) $$
パーセプトロンの各層には,配列として参照することが可能です.
network[0]は先程作成した2入力・1出力の層です.
重みを変更するには,network[0].weight.dataのfill_メソッドを利用します.
# 重みの変更
network[0].weight.data[0][0].fill_(0)
network[0].weight.data[0][1].fill_(1)
print(network[0].weight)
#出力
Parameter containing:
tensor([[0., 1.]], requires_grad=True)
バイアスを変更するには,network[0].bias.dataのfill_メソッドを利用します.
# バイアスの変更
network[0].bias.data.fill_(-0.5)
print(network[0].bias)
#出力
Parameter containing:
tensor([-0.5000], requires_grad=True)
単純パーセプトロンの入力${\bf x}=(x_1, x_2)$をテンソルとして作成します(ここではバイアスは除きます).
$$ {\bf x} = (x_1, x_2) = (1, 1) $$
# 入力
x = torch.tensor([1, 1], dtype=torch.float)
print(x)
#出力
tensor([1., 1.])
単純パーセプトロンに${\bf x}$を入力し,出力$z$を得ます.
z = network(x)
print(z)
#出力
tensor([0.6225], grad_fn=<SigmoidBackward>)
出力$z$は 0.6225 になりました. この値が正しいか確認してみましょう. 定義に従って計算すると,PyTorchで作成した単純パーセプトロンと出力が一致していることが分かります.
def sigmoid(x):
return 1 / (1 + np.exp(-1 * x))
x = np.array([1, 1, 1]) #入力
w = np.array([-0.5, 0, 1]) #重みとバイアス
y = x.dot(w) #中間出力
z = sigmoid(y) #シグモイド関数
print(z)
#出力
0.6224593312018546
課題
Google Colaboratoryで作成した chapter2.ipynb を保存し, 共有用のリンク と ノートブック(.ipynb) をダウンロードして提出してください. 提出の前に必ず下記の設定を行ってください.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定
- 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定