ニューラルネットワーク

ニューラルネットワークとは

ニューラルネットワーク（Neural Netowork） とは， 生物の脳を数理的に表現したモデルのことであり， 1943年に外科医であったウォーレン・マカロック（Warren McCulloch）氏と， 数学者であったウォルター・ピッツ（Walter Pitts）氏が考案した形式ニューロンが起源とされています．

1940年代~60年代の第1次AIブームに大きく注目され， 単純パーセプトロン と呼ばれるニューラルネットワークが提案されます． その後，1980年代の第2次AIブームにおいて， ニューラルネットワークの学習アルゴリズムである バックプロパゲーション（誤差逆伝播法） が確立し， 多層パーセプトロン へ発展します．

近年は第3次AIブームであり，ニューラルネットワークをさらに多層化させた ディープラーニング（深層学習） が提案され，画像認識などの分野で高い性能を示しています． 今後もディープラーニングは進化し，自動運転やロボット技術に応用され， 我々の生活を支える必要不可欠な技術になると予想されます． 本授業では，ニューラルネットワークの歴史を追いながら， Google Colaboratory（Colab） で実装することで，その技術を理解することを目標とします． また，ディープラーニングの実装には，Pytorch を採用します．

ニューロン

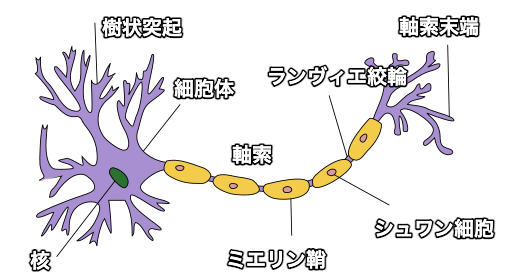
ニューロン（神経細胞）は，動物の神経を構成する細胞であり，電気的に情報を伝える役割を担っています． 入力部分が樹状突起，伝送路が軸索，出力が軸索末端となっており，他のニューロンからの伝わった刺激（電気パルス）を 変化させて次のニューロンに伝えるという仕組みになっています． 人間の脳は100億から1000億のニューロンが存在すると考えられており， 立体的で複雑な回路網が形成されているそうです． このニューロンの仕組みの数式モデルが 形式ニューロン であり， 後に発展するディープラーニングの基礎となっています．

Google Colaboratoryの基本

ブラウザでPythonの実装が可能なGoogle Colaboratoryを利用します．

ノートブックの作成

Google Colaboratoryにアクセスしたら，ノートブックを新規作成します． ノートブックを作成したら，ノートブックのタイトル（ファイル名）を設定します． 今回のタイトルは「chapter1.ipynb」としましょう．

Colabの使い方

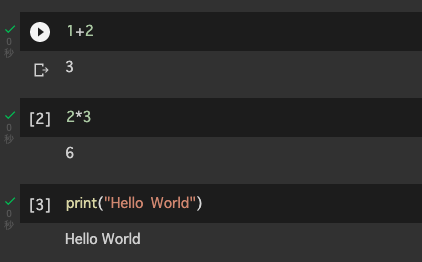
Colabではコードセルと呼ばれる入力フィールドにPythonのコードを入力します． コードセルを増やして，1+2，2*3，print("Hello World!")と入力してみましょう． 入力したらコードセルの左端にある「セルを実行」をクリックします． 実行するとコードセルの実行結果である3，6，Hello World!が出力されることが確認できます． printは文字を出力するためのPythonの命令文です． このように，適宜，コードセルを増やしながら，Pythonのコードを追加で記述して行きます．

ライブラリのインストール

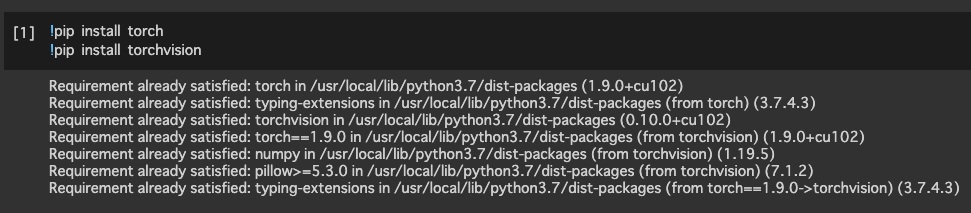
Google Colaboratoryではpipコマンドを利用して，ライブラリをインストールすることが可能です． ここでは，ディープラーニングのライブラリであるPytorch をインストールしてみます．

!pip install torch
!pip install torchvision

ライブラリのインポート

インストールしたPyTorchをインポートします． インポートとは，プログラムで該当のライブラリを利用可能な状態にすることです． 下記のコードを入力したら，Run ボタンをクリックします（Shift + EnterでもOK）．

import torch

テンソルの演算

PyTorchでは テンソル と呼ばれるデータ型を利用して，ニューラルネットワークの情報伝達を表現します． ここでは，テンソルの基本的な使い方を学びます．

テンソルの作成

1次元のテンソル（ベクトル） を作成してみます． ここで，tは変数と呼ばれ，数値や文字などの値を記憶させるために用います． また，= は代入を意味し，変数tに作成したテンソルを記憶させることを表しています． printで変数tの内容を表示します．

$$ \left( \begin{array}{ccc} 0 & 1 & 2 \end{array} \right)\
$$

t = torch.tensor([0, 1, 2])
print(t)

#出力
tensor([0, 1, 2])

2次元のテンソル（行列） を作成してみます． 2次元のテンソルは，複数のベクトルを組み合わせて表現します． ここでは，$(0,1,2)$と$(3,4,5)$の2つのベクトルを組み合わせます．

$$ \left( \begin{array}{ccc} 0 & 1 & 2 \\\
3 & 4 & 5
\end{array} \right)\
$$

t = torch.tensor([[0, 1, 2], [3, 4, 5]])
print(t)

#出力
tensor([[0, 1, 2],
        [3, 4, 5]])

テンソルの転置

テンソルの軸をtranspose()で入れ替えます（行列の転置）． 引数は入れ替える次元を指定します． ここでは，tは2次元配列と同じ構造であるため， 0番目（行）と1番目（列）を入れ替えることで転値が成立します．

$$ \left( \begin{array}{ccc} 0 & 1 & 2 \\\
3 & 4 & 5
\end{array} \right)^T = \left( \begin{array}{ccc} 0 & 3 \\\
1 & 4 \\\
2 & 5 \end{array} \right) $$

t.transpose(0, 1)

#出力
tensor([[0, 3],
        [1, 4],
        [2, 5]])

テンソルの加算

テンソルとスカラ値の加算をadd()で求めます． テンソルの各成分にスカラ値が加算されます．

$$ \left( \begin{array}{ccc} 0 & 1 & 2 \\\
3 & 4 & 5 \end{array} \right) + 1 = \left( \begin{array}{ccc} 1 & 2 & 3 \\\
4 & 5 & 6 \end{array} \right)\
$$

torch.add(t, 1)

#出力
tensor([[1, 2, 3],
        [4, 5, 6]])

テンソル同士の加算もadd()で求めることができます． テンソルの一致する$(i,j)$成分同士が加算されます．

$$ \left( \begin{array}{ccc} 0 & 1 & 2 \\\
3 & 4 & 5 \end{array} \right) + \left( \begin{array}{ccc} 0 & 1 & 2 \\\
3 & 4 & 5 \end{array} \right) = \left( \begin{array}{ccc} 0 & 2 & 4 \\\
6 & 8 & 10 \end{array} \right)\
$$

torch.add(t, t)

#出力
tensor([[0, 2, 4],
        [6, 8, 10]])

テンソルの乗算

テンソルとスカラ値の乗算をmul()で求めます． テンソルの各成分にスカラ値が乗算されます．

$$ \left( \begin{array}{ccc} 0 & 1 & 2 \\\
3 & 4 & 5 \end{array} \right) \times 2 = \left( \begin{array}{ccc} 0 & 2 & 4 \\\
6 & 8 & 10 \end{array} \right)\
$$

torch.mul(t, 2)

#出力
tensor([[ 0,  2,  4],
        [ 6,  8, 10]])

テンソルとベクトルの内積をmv()で求めます．

$$ t_1 = \left( \begin{array}{ccc} 0 & 1 & 2 \\\
3 & 4 & 5 \end{array} \right)\
$$

$$ t_2 = \left( \begin{array}{ccc} 2 & 2 & 2 \end{array} \right)\
$$

$$ t_1 \times t_2 = \left( \begin{array}{ccc} 0 \cdot 2 + 1 \cdot 2 + 2 \cdot 2 & 3 \cdot 2 + 4 \cdot 2 + 5 \cdot 2 \end{array} \right) = \left( \begin{array}{ccc} 6 & 24 \end{array} \right)\
$$

t1 = torch.tensor([[0, 1, 2], [3, 4, 5]])
t2 = torch.tensor([2, 2, 2])
torch.mv(t1, t2)

#出力
tensor([ 6, 24])

テンソル同士の内積をmm()で求めます．

$$ t_3 = \left( \begin{array}{ccc} 1 & 1 \\\
2 & 2 \\\
3 & 3 \end{array} \right)\
$$

$$ t_1 \times t_3 = \left( \begin{array}{ccc} 0 \cdot 1 + 1 \cdot 2 + 2 \cdot 3 & 0 \cdot 1 + 1 \cdot 2 + 2 \cdot 3 \\\
3 \cdot 1 + 4 \cdot 2 + 5 \cdot 3 & 3 \cdot 1 + 4 \cdot 2 + 5 \cdot 3 \end{array} \right) = \left( \begin{array}{ccc} 8 & 8 \\\
26 & 26 \end{array} \right)\
$$

t3 = torch.tensor([[1, 1], [2, 2], [3, 3]])
torch.mm(t1, t3)

#出力
tensor([[ 8,  8],
        [26, 26]])

テンソルの形状

テンソルの形状をshapeで確認します．

print(t1.shape)
print(t2.shape)
print(t3.shape)

#出力
torch.Size([2, 3]) # 2次元テンソル（行列）
torch.Size([3]) # 1次元テンソル（ベクトル）
torch.Size([3, 2]) # 2次元テンソル（行列）

テンソルのデータ型

テンソルのデータ型をtype()で確認します．

print((torch.tensor([0, 1, 2])).type())
print((torch.tensor([0.0, 0.1, 0.2])).type())

#出力
torch.LongTensor #64ビット符号付き整数
torch.FloatTensor #32ビット浮動小数点

課題

Google Colaboratoryで作成した chapter1.ipynb を保存し， 共有用のリンク と ノートブック（.ipynb） をダウンロードして提出してください． 提出の前に必ず下記の設定を行ってください．

• ノートブックの設定で「セルの出力を除外する」のチェックを外す
• ノートブックの変更内容を保存して固定
• 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定